antlr4详解

23 min read,created at 2025-06-14
antlr语法分析

在之前的文章中已经介绍过了antlr4的一些简单的使用，这次我们更加详细的介绍一遍。

背景

antlr（another tool for language recognition）是一个语言解析库，用于生成语法分析器。他用一种专用的文法的描述语言来定义编程语言，并且可以生成语法分析器，可以用于构建编程语言、DSL、表达式引擎、规则引擎等。他基于java编程语言写的，但是多种语言都可以使用他；他原理上基于LL(k)自上而下的解析方式；他支持词法分析和语法分析这两个重要的步骤，并且可以生成Listener或Visitor接口，用于处理语法分析过程中生成的结果，进一步构建属于自己的编程语言的执行流程。

antlr的安装通过pip install antlr4即可安装得到antlr4的命令行指令，但是更多的时候我们可以使用IDEA中带有的antlr4插件即可，所以这里可以先去安装IDEA的antlr4插件。

antlr需要有一个.g4后缀的文法(grammar)描述文件，例如我们创建一个T.g4文件，文件的第一行填写grammar T;代表我们创建的文法名字是T，在g4文件中，我们可以定义词法规则和语法规则，词法规则定义了词法单元，语法规则定义了语法结构，这是两个不同的部分。在执行的时候会先执行词法分析阶段，再执行语法分析阶段。

词法规则

词法规则和语法规则的定义格式都是<名称>: <规则>;，但是词法名称是大写字母开头，一般是全大写的方式，这种名称形式会被自动识别为是词法规则，如果是小写开头则会自动识别为语法规则。对于词法规则，规则部分可以定义为正则表达式，也可以定义为关键字，关键字需要用单引号括起来。例如：

T.g4
grammar T;

// 关键字要用单引号
PLUS: '+';
MINUS: '-';

// 正则表达式
INT: [0-9]+;
ID: [a-zA-Z]+;

// 忽略空格 回车等 用-> skip 表示忽略
WS: [ \t\r\n]+ -> skip;

词法规则会从输入字符串中进行各个元素的匹配，匹配成功则返回相应的Token（skip的除外），这些Token会在语法分析中进行进一步的解析。这里需要注意的是词法分析的正则写法支持是有限的，例如\d\w这种简写是不支持的，必须用[a-zA-Z 0-9_]这种集合形式，但是支持| +*?这些基础运算规则。想要表示一个规则是字符a或者b可以有以下2种写法：

R1: 'a' | 'b'; 
R2: [ab];

词法规则中，如果存在歧义。

  • 关键字有包含关系，+和++，而遇到输入++的时候，会按照贪婪的方式进行匹配，即匹配最长的++。
  • 输入同时满足两个规则的正则，例如上面R1和R2都能匹配字符a，输入a此时按照出现顺序，匹配出现在前面的规则。

语法规则

语法规则的名称以小写字母开头，一般以驼峰写法。

规则内容的形式可以是一条规则，也可以是多条可匹配的规则用|隔开，在规则内容中可以引用词法规则定义的名称，或者直接使用关键字。例如: exp: INT | INT '+' INT;定义了exp规则，可以是一个整数(INT是前面词法规则定义的)，或者一个整数加一个整数(INT '+' INT)。其中'+'是关键字，当然了，可以换成INT PLUS INT，因为PLUS已经预定义了+，两者效果一致，即使直接用+关键字，也会到预定义的词法规则中查找，并最终确认是PLUS。例如我们要定义一个赋值语句就可以这样：

varStatement: 'VAR' ID '=' exp ';'; // exp是表达式规则，这里还没有定义

在语法规则中我们同样可以使用正则，例如一个块语句内含多个其他语句：

statement: varStatement | blockStatement; // 假设只有两种语句
blockStatement: '{' statement* '}';       // 块语句中又可以有多个其他语句

这里我们就注意到了，块语句中有其他语句，就会产生一个“循环引用”，或者叫递归。在antlr4是支持部分递归的情况的，但是需要分情况讨论，对于某些间接左递归的情况是不支持的。那我们先来解释下递归的分类：

直接递归就是自己引用自己，例如：a: a '+' NUM | NUM;，而左递归就是递归的点出现在最左侧第一个元素，这里的a就是最左递归。而间接递归，就像上面的blockStatement和statement互相引用产生的递归，在两个或更多不同的规则中产生的递归，上面的例子中statement规则中的递归点出现在blockStatement他是这条分支的最左侧，而blockStatement规则中的递归点出现在statement是这条分支的中间位置。这种严格来说不算是间接左递归。（因为有一个递归点不在最左），antlr也是支持的。

说来说去antlr4好像都支持，那么什么情况下，会出现不支持的递归写法呢？我们在后面表达式规则中会看到。所以我们先来看表达式的规则。

我们以四则运算为例，如下是一种简单的递归写法，他表示表达式可以是一个数字，也可以是数字与另一个表达式用运算符连接。

grammar T;

start: exp;
exp: NUM 
    | NUM ('+'|'-'|'*'|'/') exp; 
    
NUM: [1-9][0-9]*;
WS: [ \t\r\n]+ -> skip;

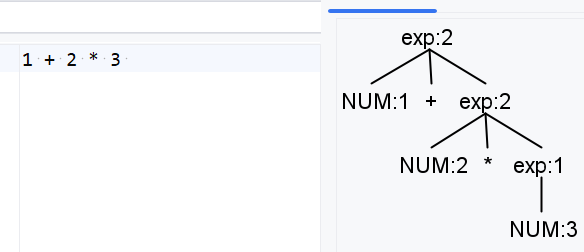
image

在当前的写法中，出现了直接递归，但是当前的写法并不优雅，exp的两个分支都是NUM开头的，这会给antlr的分支预测带来一些麻烦，好在当前情况还算简单，但确实不是一个最佳实践的写法。一种改进方式是把exp循环点的位置进行调整，即把NUM和exp互换位置：

exp: NUM 
    | exp ('+'|'-'|'*'|'/') NUM;

这样就就成了一种直接左递归的方法，即直接左递归是一种好的写法。这种写法下就没有公共的前缀了，是一种更好的写法。当然前面出现公共前缀的时候，我们还可以用正则来解决，避免出现任何递归：

exp: NUM (('+'|'-'|'*'|'/') NUM)*;

但是这种写法解析出来的抽象语法树就只有一层结构，无法解决运算优先级的问题，所以这种写法也并不适合。

image

最后看下来还是直接左递归的写法是比较合适的，那我们再来看一种写法：

exp: NUM 
    | exp ('+'|'-'|'*'|'/') exp;

这种写法出现了两个直接递归的点在一个规则分支中，这个写法在当前场景也是没问题的，但在解析的过程中可能出现歧义。例如1+2+2解析为exp(1+2)+exp(3)和exp(1)+exp(2+3)都说得过去，但是antlr是从左到右解析的，所以最终的表现是稳定的，所以这种写法也是没有问题的。

那我们接下来讨论下分支的前后顺序， 先后顺序一般的最佳实践是更复杂的规则写在前面，如果不可避免有相同前缀的，运算优先级高的写在前面。

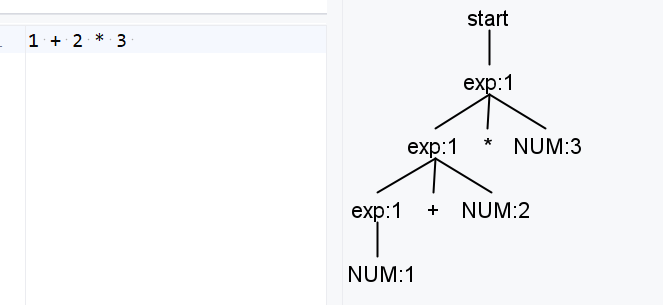
现在还有个运算符优先级的问题例如1+2*3，在解析的树状结构中，是先运算的1+2，这个优先级是不对的。因为我们把四则运算平等的当做运算符，然后左递归的原因，导致所有的运算符会按照相同优先级，并且按照左结合的方式进行运算。

image

解决优先级问题

当然如果我们采用右递归的写法会产生右结合的规则，但是无论左右都不是我们想要的，我们需要的是区分不同运算符的优先级。如何做呢？一种思路是单独把加减和乘除给拆成不同的规则。

exp: addOrSub;

addOrSub: mulOrDiv
    | mulOrDiv ('+'|'-') addOrSub
    ;

mulOrDiv: NUM
    | mulOrDiv ('*'|'/') NUM
    ;

这是一个经典的符合LL思路的写法，只看mulOrDiv这条规则，它定义了左结合的乘除法表达式，然后再看addOrSub它定义了加减法，加减法运算的每个元素是一个乘除法的元素。而每个表达式都是一个加减法表达式，这里会有疑问，我一个2*3没有出现加减法啊，但是解析的时候addOrSub的第一个分支就是只有乘除法，没有加减法的，换句话说加减法的规则是包含了乘除法。

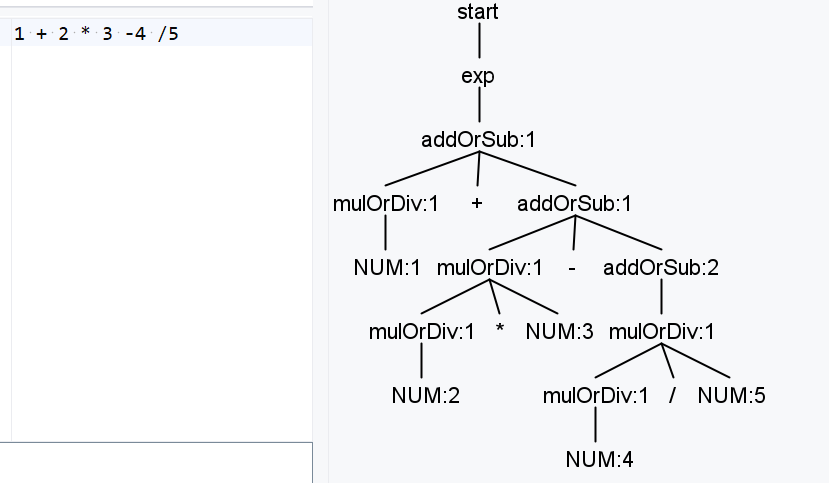
image

另外一种思路是将乘除和加减改成两个分支，而不是两个规则，并且更高优先级的乘除法需要写到前面。

exp: exp ('*'|'/') exp
    | exp ('+'|'-') exp
    | NUM
    ;

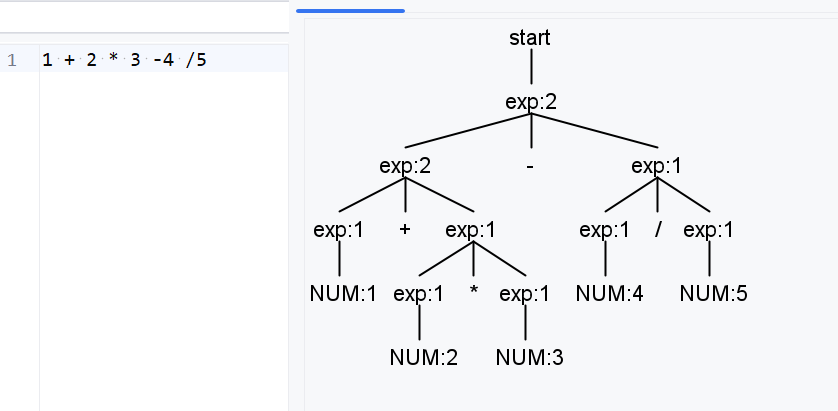
image

以1+2*3为例，在解析的时候：

  • 遇到第一个1对应会解析为exp3:NUM:1，此时成为exp+2*3
  • 遇到第二个+匹配第二条规则exp2:(exp3:NUM:1 + exp?)期望后续字符能解析为exp
  • 遇到第三个2对应解析为exp3:NUM:2，此时可以将这个exp3结果作为第二步需要的exp，但是antlr会向前多看几个字符
  • 向前看到*可以将第三步匹配成exp1:(exp3 * exp?)，和第三步进行对比，exp3:NUM:2归属问题，是归属给exp2的右节点，还是exp1左节点，显然exp1优先级更高归属给exp1。于是后续继续期望一个exp?。
  • 遇到3对应解析为exp3:NUM:3，到结尾了，不会再向前看了，所以直接作为上一步期望的exp

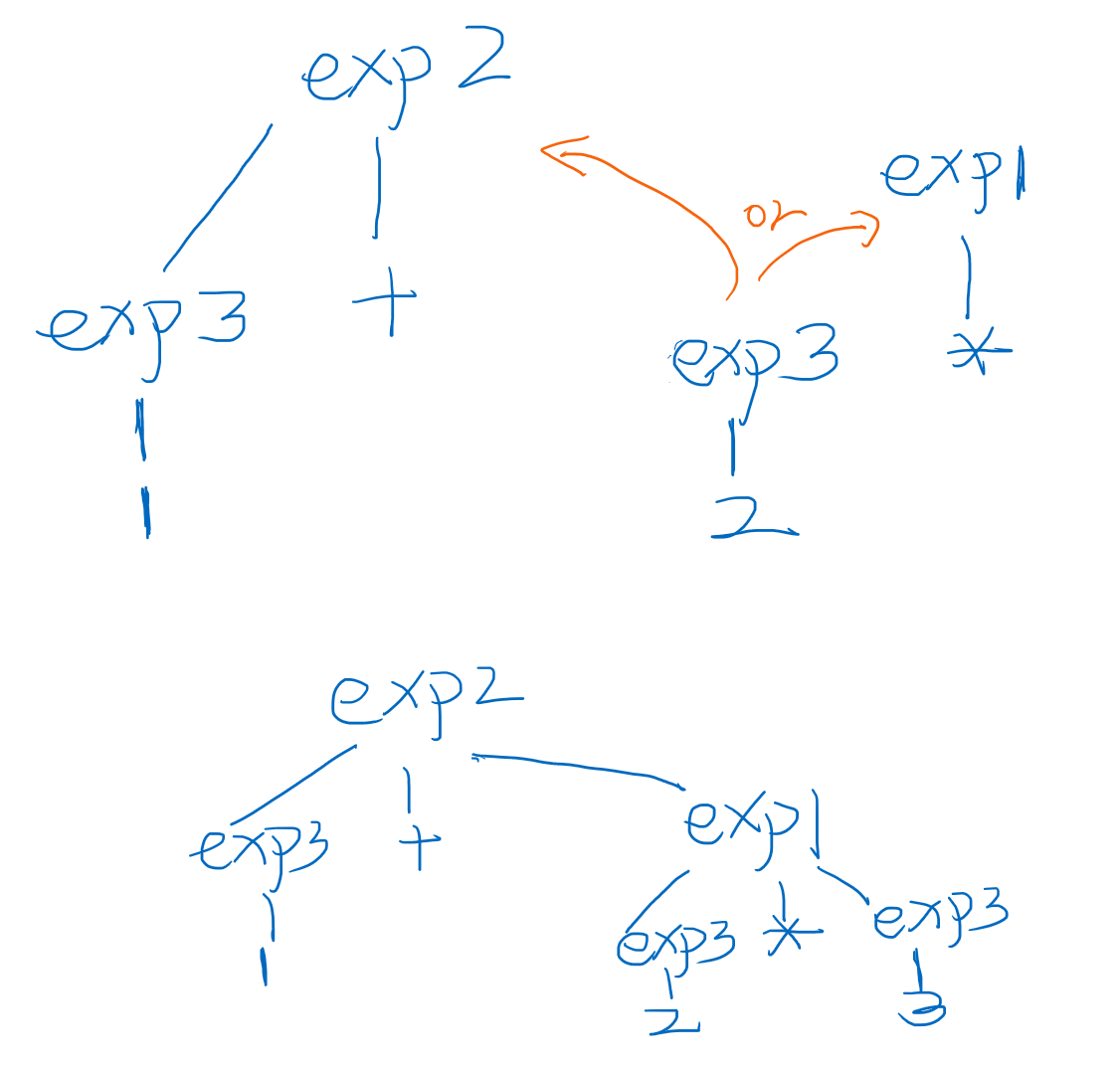
image

当输入是1+2+3的时候，2这个节点决定归属的时候左右都是exp2优先级一样，默认就会左结合了，大多数情况下都是左结合的，但是=除外，那如何解决等号的右结合呢？

解决结合问题

赋值运算符支持a=x也支持a=b=x，他是右结合即a=(b=x)，简单的语法规则如下，但是因为exp递归出现在了左侧所以结合性是左结合。

exp: exp ('*'|'/') exp
    | exp ('+'|'-') exp
    | exp '=' exp
    | NUM
    | ID
    ;
ID:  [a-zA-Z_][a-zA-Z0-9]*;

这种写法对a=b=x解析结果如下，会先运算a=b，也就是左结合，是不符合预期的。

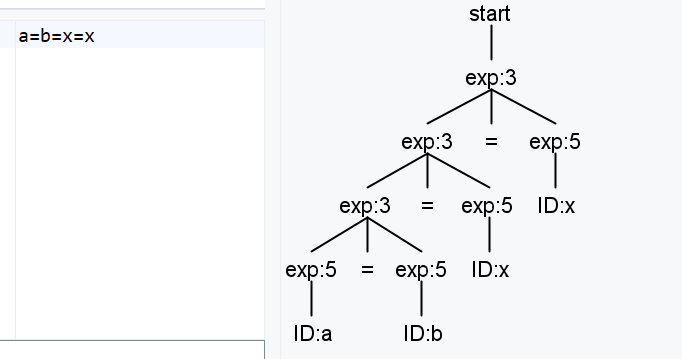
image

针对想要实现右结合的情况，一般都是因为左递归导致的左结合，一般有两种思路，把左递归改成右递归，当前这个例子中没有办法使用这个方法，因为这个例子中既有左递归又有右递归，硬要改的话，只能是让等号的左值只能取ID。

exp: exp ('*'|'/') exp
    | exp ('+'|'-') exp
    | ID '=' exp
    | NUM
    | ID
    ;

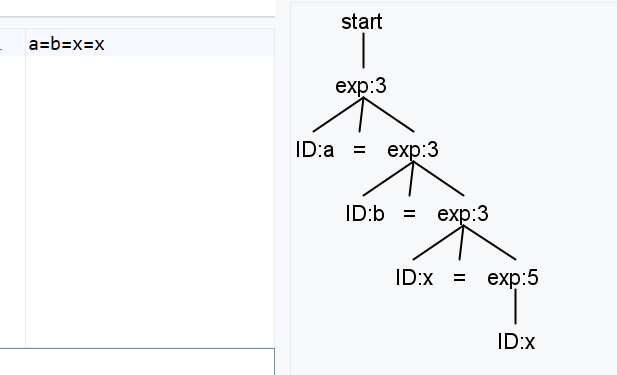
image

这样就只有一个右递归了，就会产生右结合。但是这个改动和原来不等价了，原来的写法左值可以是数字1，也可以是其他表达式1+1等。所以还有另一种解决方案，就是加一个标注：

exp: exp ('*'|'/') exp
    | exp ('+'|'-') exp
    | <assoc = right> exp '=' exp
    | NUM
    | ID
    ;

学习别人是怎么写的

这里我们学习了基本的思路，但是直接让我们来定义一门语言显然还是有些吃力，不太知道总体的结构。我们可以先来学习下别人是如何定义的。因为句子的语法定义是比较简单的，所以我们主要学习表达式expression，别人是如何定义的，这涉及到前面提到的优先级和结合性两个重要问题的解决。

Java

antlr官方github仓库中有很多编程语言的g4文件，其中java给的示例文件就是用了我们前面提到的经典LL写法来定义优先级的，代码

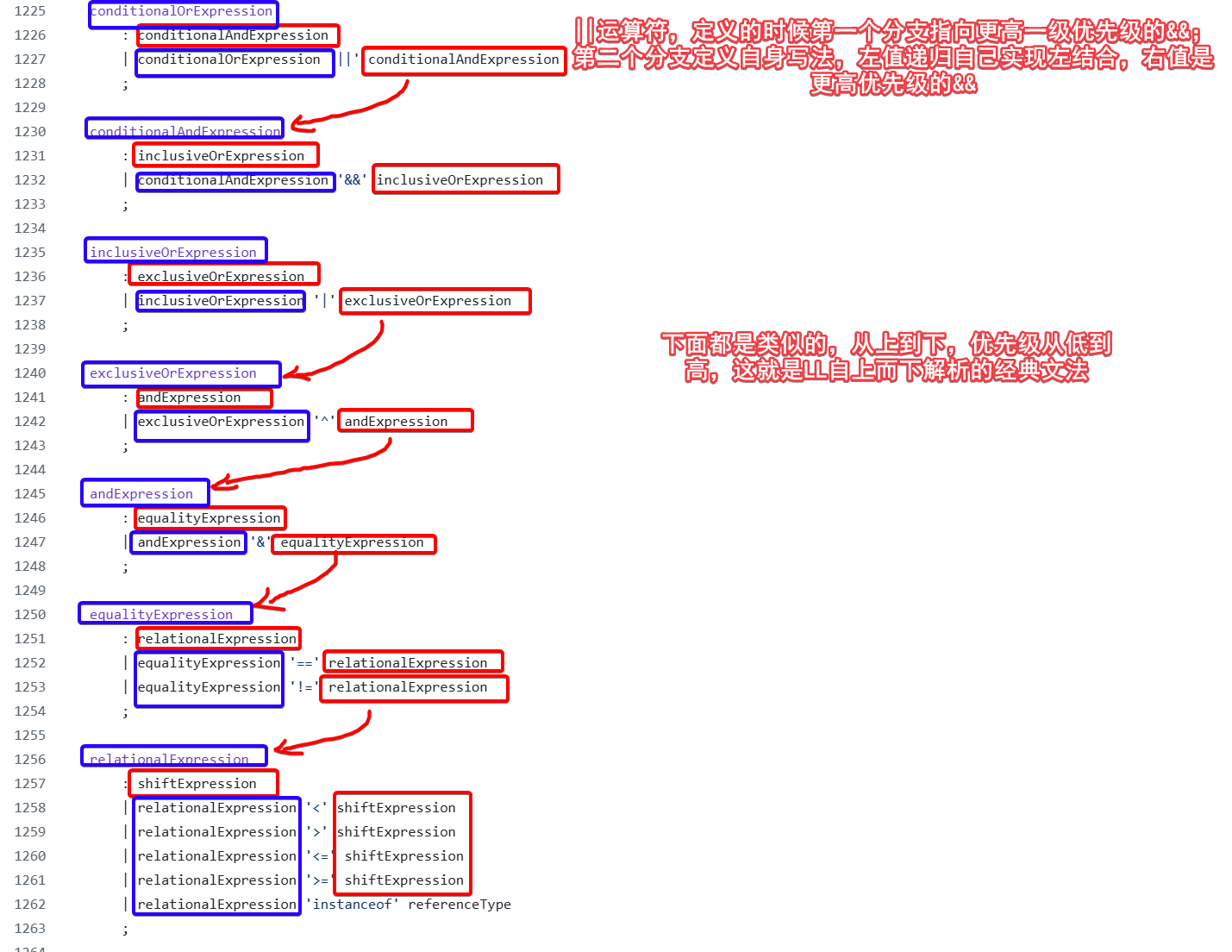
image

C

在C的示例中，同样是LL经典文法，但是形式上稍微进行了调整，也是一种不错的写法。

image

对于原来的写法，如下代表or可以是and表达式，或者是or || and而or本身是递归他可以是一个and，所以or可能是递归一次的and || and，也可能是递归两次的and || and || and，也可能是递归三次....。

or: and
    | or '||' and;

而and and || and and || and || and...也可以用正则的写法如下，这就是C这一版的改动。

or: and ('||' and)*;

Lua 与 JavaScript

上面LL写法最大的问题是，代码太长了，对于每一个优先级的运算符都要单独定义一个语法规则，并且还要引用高一个优先级的规则。就像铁锁连环一样。在antlr4中采用了LL(k)增加了更多递归场景的支持，这使得简化表达式语法规则成为了可能。

例如在Lua版本中，表达式的定义就在一条规则中将各个运算符都进行了定义。

image

同样的在js中是类似的，我们也注意到了=运算符的右结合处理就是上面我们提到的解决方法。

image

Mocha

在mocha-java项目中，我们也使用了经典的LL文法定义了我们的编程语言。因为整体结构简单，所以文件行数很少，可以拿来作为参考。

如何利用抽象语法树

上面我们已经学会了如何自己定义一个g4文件了，但是问题是我只有这个文件如何使用呢？我们可以用antlr指令来生成对应的代码文件，借助生成的代码，就可以识别一个字符串的代码输入，将其解析为抽象语法树了。后续我们就可以利用这个抽象语法树进行自己需要的操作了，例如直接解释求值，或者编译成字节码，或者是机器码等等。那么我们先来看如何生成代码吧。

# 如果安装了`antlr4` cli指令
$ antlr4 -Dlanguage=java T.g4

# 如果没安装可以直接到maven下载jar包，因为这个指令等价于antlr4='java -jar /path/to/antlr-4.x-complete.jar'
$ java -jar /path/to/antlr-4.x-complete.jar -Dlanguage=java T.g4

# 如果有IDEA插件，可以直接在IDEA右键即可搞定

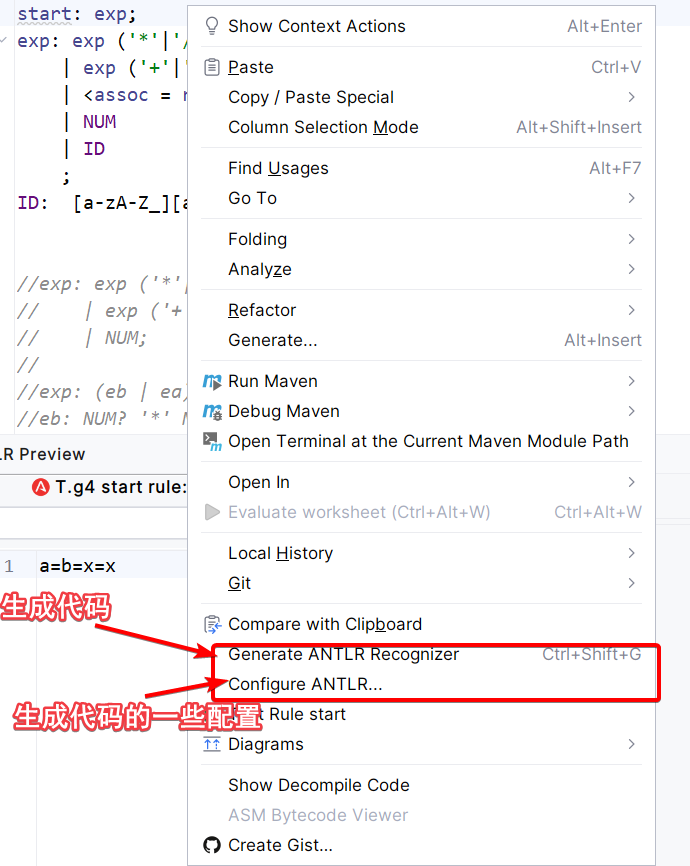
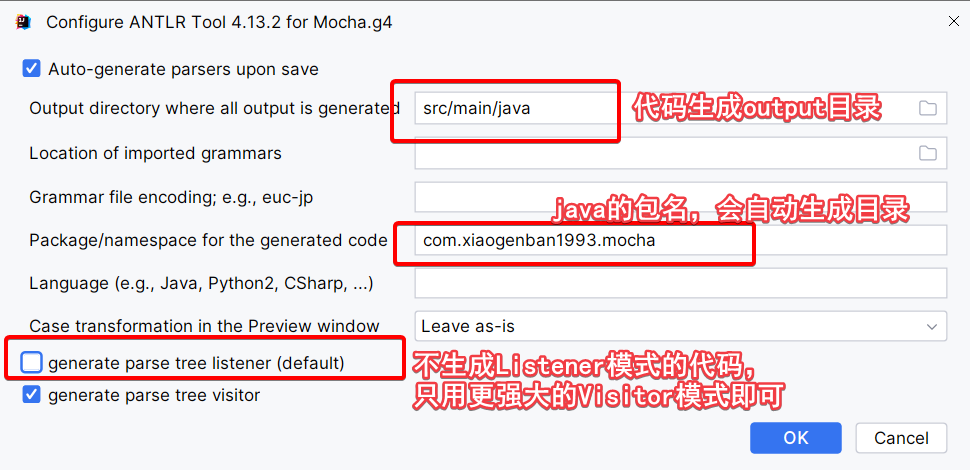
image

这里建议先进行配置，如果是生成java代码可以这样配置，如果是其他语言可以修改这里的语言和包名。

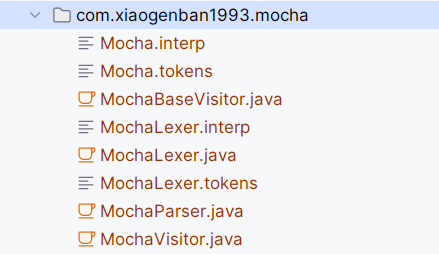
image

生成完之后，会得到如下的代码，其中.token和.interp文件是一些常量的说明和枚举可以忽略，剩下有4个java文件，其中XXLexer.java正如其名是进行词法分析的，XXParser.java是进行语法分析的，XXVisitor.java和XXBaseVisitor.java是访问者模式要用的文件，并且XXBaseListener是实现了XXVisitor接口的抽象类。

image

对于Lexer和Parser类，我们不需要做任何修改，这两个阶段的代码就是对应了我们的g4文法。而visitor是需要我们关注的，我们需要实现一个继承XXBaseVisitor的类，然后重写其中的方法，这些方法均以visit开头，对应的就是语法树中的节点，在深度遍历的时候，遍历到了当前节点。

以上面的T.g4为例

grammar T;

start: exp;
exp: exp ('*'|'/') exp
    | exp ('+'|'-') exp
    | <assoc = right> exp '=' exp
    | NUM
    | ID
    ;
ID:  [a-zA-Z_][a-zA-Z0-9]*;

我们可以重写的方法如下，

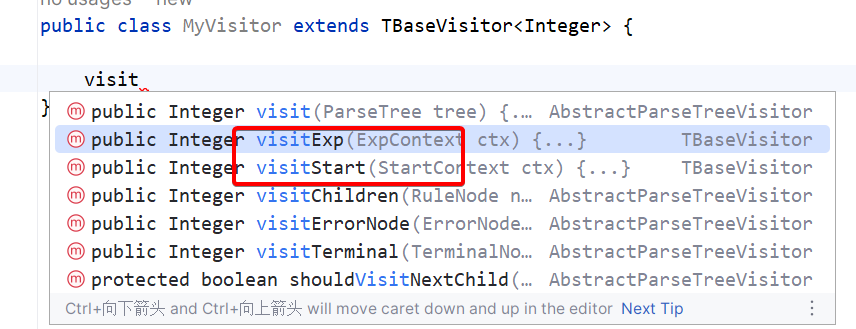
image

当然其中最主要的就是visitExp方法，因为这是我们唯一的一个语法规则。其中ID方法是当匹配ID这个分支的时候，可以拿到对应的值，但是我们没法知道当前具体匹配的是哪个分支，所以需要对g4文件添加标注。

imag

grammar T;

start: exp;
exp: left=exp ('*'|'/') right=exp                  # mulDiv
    | left=exp ('+'|'-') right=exp                 # addSub
    | <assoc = right> left=exp '=' right=exp       # assign
    | NUM                               #  num
    | ID                                # id
    ;
ID:  [a-zA-Z_][a-zA-Z0-9]*;

有了标注之后，visitExp方法就会被拆解为五个方法：

image

这样我们就可以针对每一种情况分别处理了。例如一个简单的四则法运算的求值，就这样完成了。

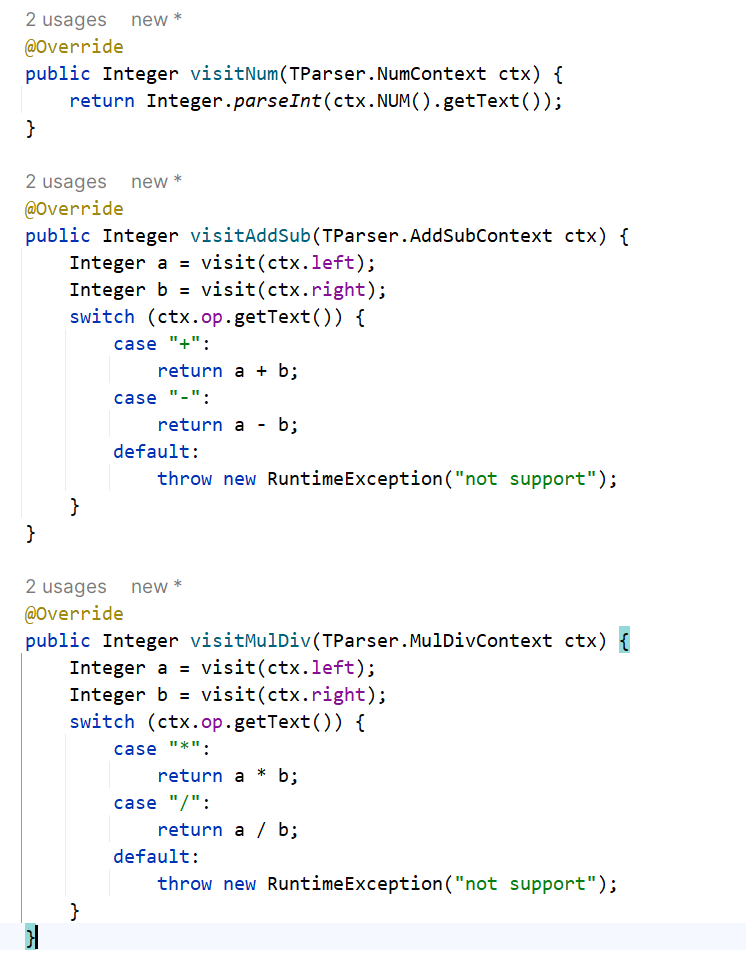
image

visitXX方法的默认实现是对ctx中包含的其他子ctx节点进行visit，只有重写才能发挥作用，否则就是遍历一遍，不做任何事情。然后我们写主程序来触发代码的解析与执行：

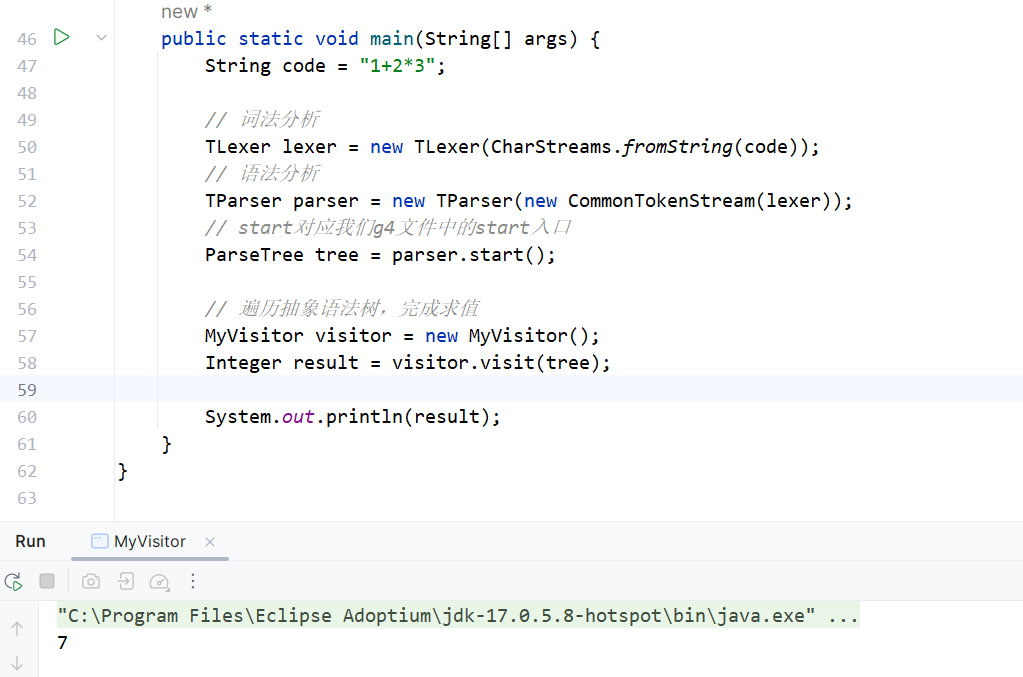
image

当然这个例子比较简单，更为完善的例子可以参考。在这个代码中，我们定义了自己语言的数据类型Element。以及在这个项目中，我还尝试了不进行解释求值，而是编译成字节码，当然这里我没有再去定义一套字节码规范，而是把程序编译为jvm字节码，即class文件了。参考这个目录下的实现